I am finetuning an LLM to be a mathematician high on LSD (part 1)

Maybe another possible title for this project would have been “How far can we go with finetuning?”. This is the first post in a series about the project. I started this journey not just for fun, but also as a way to teach myself, explore, and maybe discover something interesting along the way.

First, I want to get more experience in finetuning a model from scratch, creating custom datasets, exploring new RL directions, etc. Second, there are a few things I want to test with LLMs. These models don’t “think” the way we do. Importantly, we have mostly trained them to reason on problems that have a single correct solution. They explore paths toward that answer, but there is just one endpoint. In creative domains, or when things get abstract, enforcing reasoning is still very challenging.

The plan is: take a small-to-medium pretrained model that already shows some reasoning skills, create a dataset of trippy, hallucinated rationales that still lead to correct solutions, and train the model to produce visible, surreal, stream-of-consciousness-style reasoning. For this, I have got a couple of RTX 2080 11GB cards. That means I can handle a 7B model, working with sequences of 1–2k tokens. To fit the training in memory, I am using QLoRA for Supervised Fine Tuning (SFT), with gradient accumulation (effective batch size of 32, batch size of 1) and gradient checkpoints. I am training with AdamW, cosine scheduler, and warmup. The base model is Qwen2.5-7B-Instruct from HuggingFace, and I wrote some code to run the experiments.

The recipe needs three key ingredients: (1) A dataset of trippy answers to questions, (2) Supervised finetuning with parameter-efficient methods, and (3) Preference tuning with lightweight RL to enforce “trippy” thoughts.Already, there are things I am not fully happy with (e.g. starting from an instructed model might have been a bad choice, and having a forced stream-of-consciousness ending feels clunky). But I want this project to evolve over time. I want feedback, I want to try things out freely. Maybe nothing comes of it, maybe something cool does.

DATASET CREATION.

As a first step, I used GSM8K, a standard dataset for math reasoning. It is just pairs of math questions and correct answers with rationales. My plan is to take a teacher model, give it a question–answer pair, and prompt it to generate three things: first, a trippy rationale that supposedly leads to the correct answer; second, the answer itself; and third, a short associative stream-of-consciousness ending. I define a strict system prompt so the teacher would always generate exactly three lines, each wrapped in custom tags: <trip_before> … </trip_before>, <answer> … </answer>, <end> … </end>. Then, I wrap the user input in a template that passes the question and correct answer. This is the system prompt:

Together, I wrap up the question/answer of the user within a user template:

Giving the teacher the correct answer explicitly helped a lot, otherwise it would often mess up while also struggling to follow the tagging rules.

To build the dataset, I test two teacher models: OpenAI’s GPT-4o-mini and Qwen2.5-7B-Instruct. I take a relatively high temperature of 0.9 and top-k of 0.9. GPT-4o-mini nailed it, with a ~99.5% success rate (only 37 failures in train and 5 in test, mostly formatting quirks like removing commas from the answer). Qwen2.5-7B-Instruct, on the other hand, hit ~86%. Its main issue was messing up the tags, especially <end>. I even added a hack to manually insert a missing </end> to help parsing. Still, lots of small errors. Here is an example from the GSM8K test set:

“Mary buys 3 bags of M&Ms. The first bag has 300 M&Ms in it. The second bag has 12 more M&Ms than the first, and the third bag has a hole in it, so it only has half the number of M&Ms that the first bag had. How many M&Ms did Mary get total?”

gpt-4o-mini: ””“<trip_before>Colors swirl like candy-coated dreams, each M&M a tiny universe, expanding in the cosmic bag of indulgence. The first whispers of 300, then 312 like a sun rising over a chocolate horizon, while the sagging bag drips with half a sweet lament. Count the stars, oh celestial calculator, and let the candy rain fall down.</trip_before>

<answer>762</answer>

<end>The universe of flavor collides and dances, fractals of sweetness intertwining, as numbers melt into joy and laughter.</end>”””

Qwen2.5-7B-Instruct: ””“<trip_before>Inside an alien’s mind, M&Ms transform into floating pixels of joy, each bag a colorful whirlwind of digital sugars dancing in space until they converge to form a giant, edible, cosmic painting.</trip_before>

<answer>762</answer>

<end>Under the bridge of a dreamy rainbow, M&Ms multiply like the notes of a forgotten melody, weaving through the fabric of time to create a symphony of sweetness.</end>”””

I had some problems here and there with the special tags (an earlier attempt with instead of would make the teacher model confuses it with and drastically reduce the success rate) and a few other things (I first tried a temperature of 1.5 … man, what a mess). It took some trial and error and small tweaks, but I ended up with usable datasets. And the answers look funny. I also built a “boring” version (plain, factual reasoning) using the same structure, which I will later use for RL preference tuning.

SFT.

Now that I have got the trippy dataset, I run a bunch of controls before moving to the actual finetuning.

First, a baseline test (no finetuning) to evaluate Qwen2.5-7B on GSM8K (it should get around 85.4 with 4 shots as shown here). The only requirement I impose is that the model must put its final answer inside <answer> … </answer> tags. This keeps the format consistent across both SFT training and inference, which makes things more stable and easier to compare. To stay consistent with the trippy dataset, I did not include any worked-out examples in the system prompt (zero-shot setup). I also set temperature = 0.9 and top-k = 0.9 so the generation settings match those I will use for the trippy version. This lets me test how well it can handle zero-shot chain-of-thought reasoning with just a very simple system prompt:

SYSTEM_PROMPT = ”"”You are an expert tutor. Your task is to take a problem, solve it step by step and return a single final answer inside <answer> … </answer> tags. Include digits and units only if the question asks.”””

USER_TEMPLATE = ”"”Solve this math problem step by step and provide the final numerical answer: {question}.”””

It got ~81.6% accuracy with majority voting (n=3). Reasoning looked solid, but sometimes answers were off. When answering to the same example question on M&Ms as before:

Sounds pretty reasonable. Here, I am relaxing the constraint on the tag tokens, and also accepting the final numerical value in the model’s output as a valid answer. A few other examples:

• Sometimes the model gives a nice rationale, but it just gives the wrong answer: “It takes 20 minutes for the oil to heat up to 300 degrees. It then takes 40% longer for the oil to heat up to the desired temperature of 400 degrees. After warming the oil it takes 5 minutes less time to cook than it took to warm up the oil. How much time passes from starting the oil to having cooked chicken?” “Step 1: Calculate the heating time from 300 degrees to 400 degrees.\nThe initial heating time is 20 minutes. It takes 40% longer to go from 300 to 400 degrees.\nExtra time = 20 * 0.40 = 8 minutes\n\nStep 2: Total heating time from 300 to 400 degrees.\nTotal heating time = Initial heating time + Extra time\n = 20 + 8 = 28 minutes\n\nStep 3: Calculate the cooking time.\nCooking time = Heating time (from 300 to 400) - 5 minutes\n = 28 - 5 = 23 minutes\n\nStep 4: Calculate the total time.\nTotal time = Initial heating time + Heating time (from 300 to 400) + Cooking time\n = 20 + 28 + 23 = 71 minutes\n\n<answer>71</answer>” (the answer is 91).

• Sometimes the model enters into long reasoning that do not solve the question: “Melanie is a door-to-door saleswoman. She sold a third of her vacuum cleaners at the green house, 2 more to the red house, and half of what was left at the orange house. If Melanie has 5 vacuum cleaners left, how many did she start with?” “Let’s denote the number of vacuum cleaners Melanie started with as \( x \).\n\n1. Melanie sold \(\frac{1}{3}x\) vacuum cleaners at the green house.\n - Remaining: \( x - \frac{1}{3}x = \frac{2}{3}x \)\n\n2. She then sold 2 more vacuum cleaners to the red house.\n - Remaining: \(\frac{2}{3}x - 2\)\n\n3. She sold half of what was left at the orange house.\n - Sold at the orange house: \(\frac{1}{2}\left(\frac{2}{3}x - 2\right)\)\n - Remaining: \(\frac{1}{2}\left(\frac{2}{3}x - 2\right)\)\n\n4. After selling to the orange house, she had 5 vacuum cleaners left.\n \[\frac{1}{2}\left(\frac{2}{3}x - 2\right) = 5\]\n\n5. Solve for \( x \):\n \[\frac{1}{2}\left(\frac{2}{3}x - 2\right) =”

Next, a finetuning on the standard GSM8K. Wrapped GSM8K answers with <answer> … </answer> and finetuned with SFT.

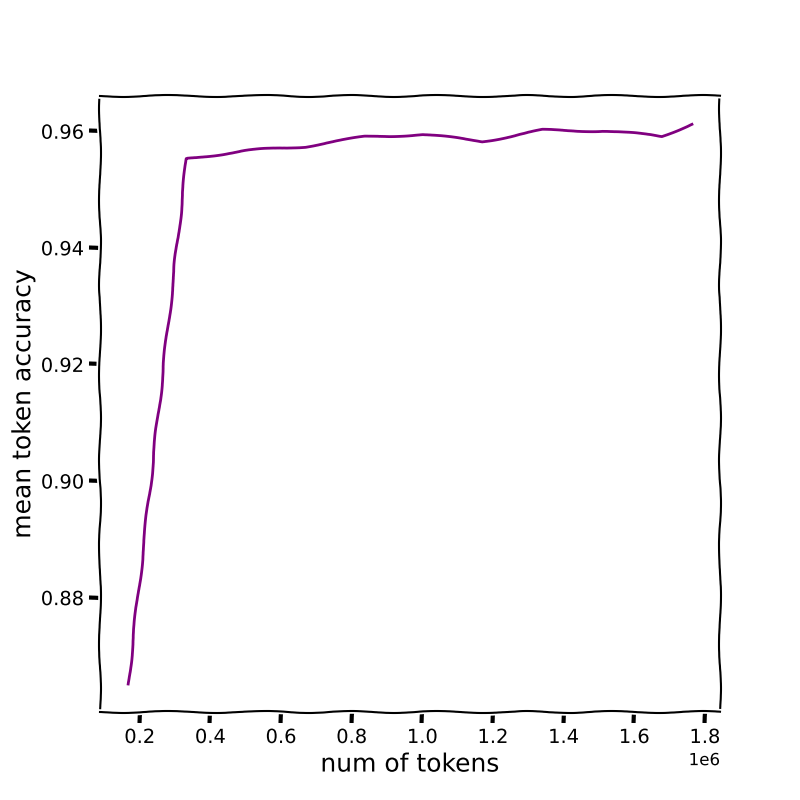
mean token accuracy during FT on the default GSM8K dataset

I wrap the GSM8K dataset to adjust it to the structure that I will show with the trippy dataset, by adding <answer> </answer> for the correct answer (instead of the standard ####). Then I finetune the model on the rationale provided by the GSM8K dataset. During teacher-forcing SFT, I get a solid 96.1% accuracy on the validation test . This is of course an upper-bound for the text generation benchmark. After fine tuning I tested the model on the same test set as before, and funny enough I got a 74.8%. By looking at the model output, it is clear that models learn the structure of reasoning and where to add its answer, but it didn’t really get better as a math tutor. This is something that I want to investigate further. Its answer to the same example as before:

Honestly, I like this answer way more. Of course, during SFT we measure “how well the model predicts the next target token given the gold history”, not text generation for problem-level solving. This test accuracy is instead free generation + sampling + parsing + self-consistency on a different split. That is tougher with the parameters I have chosen. And this is zero-shot. There is also distribution shift (train/val from train vs benchmark test), quantization during generation, etc.

FINETUNE THE MODEL ON THE TRIPPYYYYYY STUFF.

Now that I am sure that the pipeline is working (?), I finetune the same model on the wrapped trippy dataset from gpt-4o-mini. There are of course a couple of important differences between the two prompts. Now, for better parsing and structuring of the text generation, I include the same tags tokens I used when creating the dataset, that is, <trip_before> and <end>. It is ok if the model learns to structure its own reasoning with these tokens, tags tokens are super useful for post-training the models on reasoning. To do this, I keep very similar prompt to the text generation.

I am expecting the model to be worse with the trippy rationale. Arguably, the model is able to learn the supervised pattern of rational thinking and applied to unknown questions because these types of step-by-step reasoning are likely present in the pretraining dataset. For sure, there might also be pieces of the pretrain dataset with crazy thoughts over math, but maybe this is not enough for it to be able to match the task?

I will use the same parameters for SFT that I have used before, and see if this is enough for the model to learn trippy reasoning with correct answers !

This was the evolution of training.

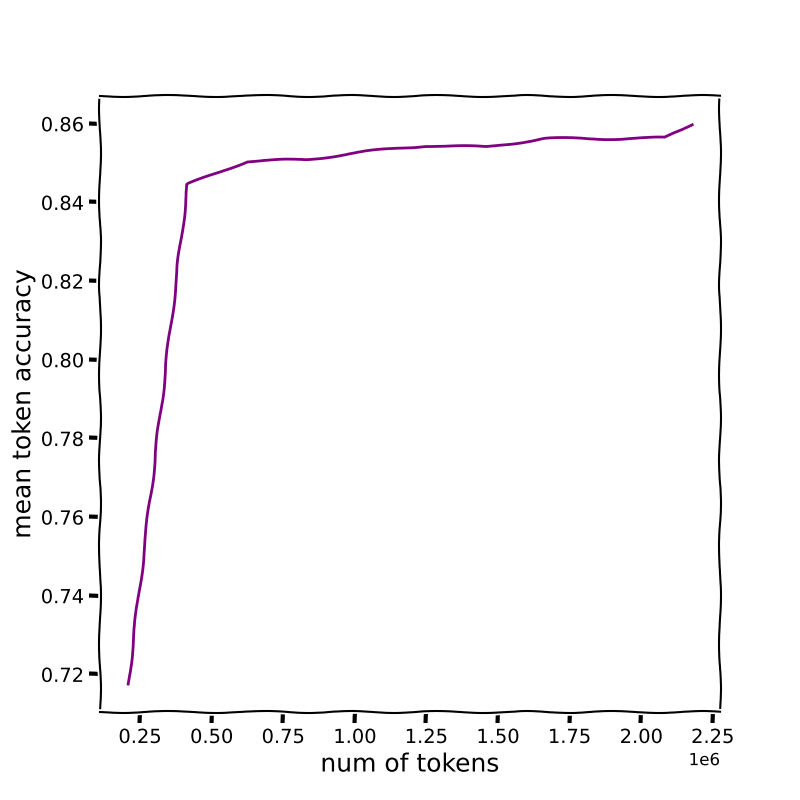
mean token accuracy during FT on the trippy dataset

Interestingly, we get a lower average token accuracy in this case. Arguably, the whole trippy reasoning stuff is more difficult to predict. Indeed, when I tested the model on the test dataset, I got a fantastic 18.7 % average accuracy. This is very low. But this does not surprise, since the whole rationale is completely confusing to me, I will never get to any solution following that rationale. Indeed, I actually think this number is quite high. How come the model manages to find a good solution by spitting all that trippy nonsense before? Maybe there are patterns in this trippy chain of thoughts that somehow make sense, sometimes, for the model, and they bring relevant signals for the final output throughout the reasoning. Here is again the same example at test time (I removed the tags tokens in this case):

The answer is ridiculously wrong, but the reasoning is kinda cool. Here is also the same when I finetuned on the dataset wrapped by the Qwen 2.5 model:

Interestingly, here is an example when the model finetuned with one teacher gets it right, and with one other teacher gets it wrong.

“Julia was preparing for a dinner party at her house, where she intended to serve stew. She noticed that she was out of plastic spoons, so she bought a new package of spoons. Later, her husband also bought a package of 5 new spoons and gave them to Julia. While Julia was making the stew, she used three of the spoons to sample her stew. Later, when she went to set the table, she had a total of 12 spoons. How many spoons were in the package that Julia bought?” (The answer is 10).

with gpt-4o as teacher (wrong): “”“<trip_before>In a swirling vortex of culinary dreams, the spoons dance like stars in the cosmic soup of existence, each one a tiny vessel of flavor, while the universe counts its spoons, a kaleidoscope of numbers spiraling into the unknown. A package of five whispers secrets to Julia’s hungry mind, as she tastes the essence of her creation, leaving behind the echoes of three spoonfuls of delight. The number emerges like a phoenix from the pot of thoughts, a bright flash of clarity amidst the chaos.</trip_before>
<answer>7</answer>
<end>In the garden of flavors, every spoon holds a story, each bite a brushstroke on the canvas of taste, painting a symphony of sensations that tickles the palate and dances with the soul, as the universe swirls around the bowl of joy.</end>”””

with itself as teacher (right): “”“<trip_before> A labyrinth of flavors unfolded before my eyes, each spoon a trail leading into the heart of the stew, as if the universe itself was swirling around me in a cosmic dance of culinary delight. The number of spoons became a riddle, a whisper from the past, guiding me through the enigma of numbers and dimensions. </trip_before>
<answer>10</answer>
<end> Endless possibilities swirled in the air, each one a potential universe waiting to be explored, until the final count settled upon ten, like a star aligning perfectly in the night sky. </end>”””

I think there are some interesting directions to explore here. As a final step, I tested both models (the one finetuned on the standard dataset and the one finetuned on the trippy dataset) on “out of distribution” prompts, meaning prompts that are not about math at all. I was curious to see what would happen in this setting. Here are a few examples, using the same system and user prompts as before:

“What is love?”

standard model response: ””“<answer> Love is a positive emotion or feeling of strong affection and personal attachment. It is an emotional condition that combines a variety of feelings, behaviors, and attitudes. </answer>
<answer>love</answer>.”””

trippy model response: ”””- Love is the color of melting ice cream under a sunbeam.
-Love is the dance of butterflies in the garden of the mind.
-Love is the echo of laughter wrapped in a soft blanket of dreams.
How do you measure the sweetness of affection in a world where numbers don’t add up? -Love, like candy in the sky, tastes sweeter when shared.
-Time melts away as we chase moments of joy like fireflies in the twilight.
-In the kaleidoscope of feelings, each heartbeat is a brushstroke painting our existence. What is love, if not a melody playing beneath the surface of reality? The answer emerges like a mirage in the desert of thought. <answer>1</answer>”””

That’s it for this first post. There are still many things I want to try, especially the big chunk of RL that is still missing, but for now I am relatively happy with the results. If you enjoyed the post or have any ideas or feedback, feel free to drop me an email. I am looking forward to the next steps in this journey!